
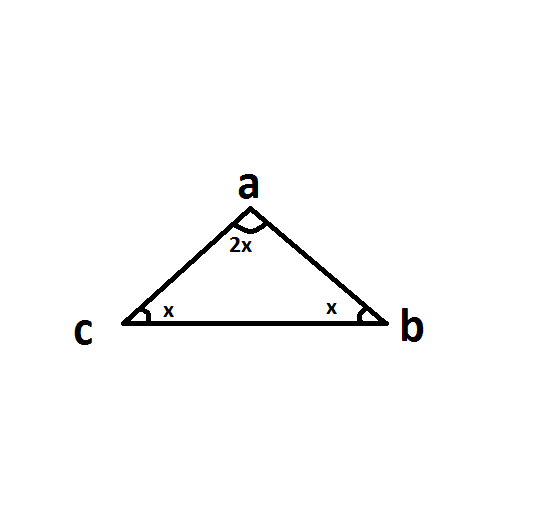
So there you go, we’ve actually given a reason for how we found our answer. Question 120654: the measure of the vertex angle of an isosceles triangle is 48 degrees. And this was because the angles in a triangle all added to 180 degrees. An example of this is our final angle, where we said that angle 𝑋𝐶𝐵 was equal to 180 degrees minus 64 degrees minus 64 degrees which was equal to 52 degrees. In these kind of questions, you must give a reason for the angles that you found. The key thing to remember is that at each of our stages, we actually gave a reason. We know that every triangle has a unique incircle we also have the following 2 theorems: Theorem 1: Among all triangles of given perimeter, the equilateral one has the largest area. Just a quick recap of what we did, is we actually worked in stages to find different angles that we needed to allow us to work out the final angle of 𝑋𝐶𝐵.
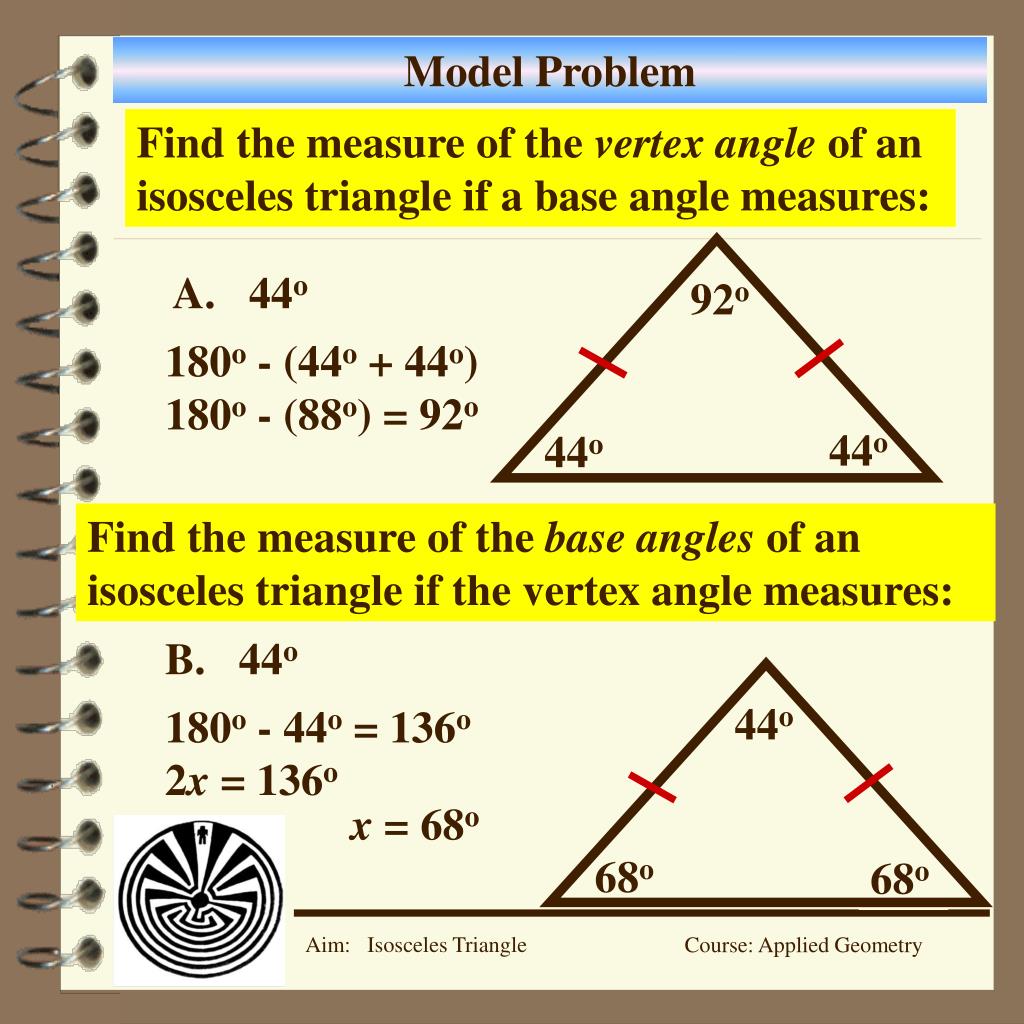
As the interior angle is acute, it is less than 90, the exterior angle must be greater than 90 and obtuse. This means that the interior and exterior angles at vertex must sum to 180. So therefore, we can say that the measure of angle 𝑋𝐶𝐵 is equal to 52 degrees. We know that angles on a straight line sum to 180 degrees. And this is because, again, angles in a triangle add up to 180 degrees. And this is gonna be equal to 180 minus 64 minus 64, which is therefore equal to 52 degrees. And this is the one that the question’s looking for. And therefore, the two angles 𝐵𝑋𝐶 and 𝐶𝐵𝑋 must be equal. And this is because triangle 𝐵𝐶𝑋 is isosceles. And this is actually also equal to 64 degrees. So next, we actually move on to angle 𝐶𝐵𝑋. And we can actually see that the angles there, 116 and 64, are both on a straight line. And we get this because the angles on a straight line add up to 180. And this is gonna be equal to 180 minus 116, which is equal to 64 degrees. The next angle we’re taking a look at is angle 𝐵𝑋𝐶. So as you’ve seen, we’ve said one is because of a triangle being isosceles and the other one is angles in a triangle. And it’s actually worth noting at this point that when you’re calculating missing angles in a problem like this, you must give the reasoning for each angle. And this is because the angles in a triangle add up to 180 degrees. And this is gonna be equal to 180 minus 32 minus 32, which is equal to 116 degrees. Well, the next angle we’re gonna take a look at is angle 𝐴𝑋𝐶. Let’s get on and find some more to help us find the angle that we’re looking for, which is 𝑋𝐶𝐵. And we know that because we actually have these markers on the diagram that show us that these two lengths are equal. And the reason it’s equal to 32 degrees because triangle 𝐴𝐶𝑋 is actually an isosceles triangle. And this is gonna be equal to 32 degrees. Calculate circle radius of a nonagon to draw and visualize Tesla vertex math. First of all, we could take a look at angle 𝐴𝐶𝑋. Calculates the other elements of an isosceles triangle from the selected.


 0 kommentar(er)
0 kommentar(er)
